



Next: Analysis of Harmonics
Up: SigSpec User's Manual by
Previous: Time-resolved Analysis
Contents
SIGSPEC AntiAlC: Anti-aliasing Correction Mode
In AntiAlC mode, SIGSPEC does not follow a strict step-by-step prewhitening sequence. Instead, test runs are performed for a number of candidate peaks in the significance spectrum in order to find the solution that produces a minimum residual rms scatter after a user-given number of prewhitenings.
- All peaks above a given sig limit are taken into consideration. The keyword antialc:par in the .ini file is followed by a floating-point number. This quantity is the AntiAlC parameter
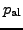 , which has to attain a value in the interval
, which has to attain a value in the interval
![$\left] 0,1\right]$](img116.png) . If the highest sig in the considered frequency range is
. If the highest sig in the considered frequency range is
![$\max\left[\mathrm{sig}\left( A\right)\right]$](img117.png) , then the sig limit is
, then the sig limit is
![$p_\mathrm{al}\max\left[\mathrm{sig}\left( A\right)\right]$](img118.png) . I.e., the AntiAlC parameter determines the sig limit for the candidate peak selection relative to the highest peak in the spectrum under consideration. Alternatively or in addition, a sig threshold for the AntiAlC candidate selection may be defined using the keyword antialc:siglimit. If neither antialc:par nor antialc:siglimit are present, the sig limit specified by siglimit in the .ini file (p.
. I.e., the AntiAlC parameter determines the sig limit for the candidate peak selection relative to the highest peak in the spectrum under consideration. Alternatively or in addition, a sig threshold for the AntiAlC candidate selection may be defined using the keyword antialc:siglimit. If neither antialc:par nor antialc:siglimit are present, the sig limit specified by siglimit in the .ini file (p.![[*]](file:/usr/share/latex2html/icons/crossref.png) ) is used for the AntiAlC candidate selection also.
) is used for the AntiAlC candidate selection also.
- The candidate selection is performed for each step in the test prewhitening sequence.
- The resulting procedure is the computation of all combinations of candidate peaks above a sig threshold determined by the AntiAlC parameter. The number of iterations for these test prewhitenings is determined by the keyword antialc:depth, followed by an integer value. It specifies the depth of the AntiAlC computation.
- The successful combination of peaks is selected upon the minimum residual rms deviation out of all examined combinations.
- SIGSPEC does not necessarily adopt all iterations performed in the test run for the main prewhitening cascade. The integer value following the keyword antialc:adopt determines how many prewhitening steps shall be adopted. This quantity must not exceed the computation depth provided by the keyword antialc:depth. If the limits specified by the keywords iterations, siglimit, or csiglimit are reached, the output may even terminate before the number specified by the keyword antialc:adopt.
According to Reegen (2007), the expected sig is approximately proportional to the squared amplitude, if all influences by the time-domain sampling are neglected. The combination of 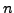 sinusoidal signal components interacting via aliasing is expected to produce a maximum amplitude that does not exceed the sum of amplitudes of the sinusoidal components. Consequently, the square root of the sig of such a combination,
sinusoidal signal components interacting via aliasing is expected to produce a maximum amplitude that does not exceed the sum of amplitudes of the sinusoidal components. Consequently, the square root of the sig of such a combination,
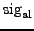 , is very likely below the sum of square roots of individual sigs
, is very likely below the sum of square roots of individual sigs
 ,
,
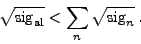 |
(12) |
If these all are assumed equal and denoted
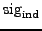 , then the upper sig limit for the alias is
, then the upper sig limit for the alias is
 . In other words, if a given peak with a sig
. In other words, if a given peak with a sig
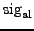 is an alias of a combination of
is an alias of a combination of 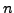 signal components with unique sigs
signal components with unique sigs
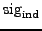 , then the individual significances are probably higher than
, then the individual significances are probably higher than
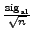 . In terms of the AntiAlC parameter, one obtains
. In terms of the AntiAlC parameter, one obtains
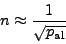 |
(13) |
for the approximate number of signal components that can be assigned alias-free for a given AntiAlC parameter 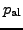 . Based on these considerations, SIGSPEC evaluates the AntiAlC computation depth using the AntiAlC parameter, if the keyword antialc:depth is not provided in the .ini file.
. Based on these considerations, SIGSPEC evaluates the AntiAlC computation depth using the AntiAlC parameter, if the keyword antialc:depth is not provided in the .ini file.
The AntiAlC mode produces additional screen output, if a combination of candidate peaks yields a lower residual scatter than the previous minimum, a two-line screen message is returned. The first line is a set of indices. In the example below, the AntiAlC parameter (keyword antialc:par) is set 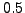 , and the AntiAlC computation depth (keyword antialc:depth) is
, and the AntiAlC computation depth (keyword antialc:depth) is 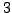 . Correspondingly, the first line of output applies to the first of altogether ten candidate peaks in the first iteration, the first out of three in the second iteration, and the first out of seven in the third iteration. This peak constellation produces an rms deviation of residuals as displayed in the second line of output (in the example
. Correspondingly, the first line of output applies to the first of altogether ten candidate peaks in the first iteration, the first out of three in the second iteration, and the first out of seven in the third iteration. This peak constellation produces an rms deviation of residuals as displayed in the second line of output (in the example
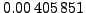 ). After finishing the test cascade, the number of iterations specified by the keyword antialc:adopt (in the present example, this number is
). After finishing the test cascade, the number of iterations specified by the keyword antialc:adopt (in the present example, this number is 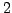 ) is adopted for the main cascade. The screen output produced by the main cascade is the same as for a normal SIGSPEC prewhitening cascade without AntiAlC. The files containing spectra and residuals, respectively, are updated each time the residual rms deviation improves.
) is adopted for the main cascade. The screen output produced by the main cascade is the same as for a normal SIGSPEC prewhitening cascade without AntiAlC. The files containing spectra and residuals, respectively, are updated each time the residual rms deviation improves.
Figure 21:
Time series used for the sample project antialc (dots). The sampling represents 14 nights of Strømgren  photometry of the
photometry of the 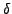 Sct star 4CVn, acquired in February and March, 2007. The magnitude values are synthesized forming two sinusoidal signals (solid line) plus Gaussian noise.
Sct star 4CVn, acquired in February and March, 2007. The magnitude values are synthesized forming two sinusoidal signals (solid line) plus Gaussian noise.
|
|
Example.![[*]](file:/usr/share/latex2html/icons/footnote.png) The sample project antialc illustrates the anti-aliasing correction using the same sampling as the data for the sample project timeres (p.
The sample project antialc illustrates the anti-aliasing correction using the same sampling as the data for the sample project timeres (p.![[*]](file:/usr/share/latex2html/icons/crossref.png) ),
),
- a sinusoid with frequency 6.5598 cycles per day, amplitude 7.29 mmag,
- a sinusoid with frequency 8.5637 cycles per day, amplitude 6.87 mmag,
- Gaussian noise with 7.36 mmag rms deviation,
as displayed in Fig.21 . The two signal frequencies differ by almost exactly 2 cycles per day and may easily be misidentified as aliases of each other. There are two identical versions of the light curve provided for comparison: alc.dat and antialc.dat.
Figure 22:
Fourier spectra for the sample project antialc. Left: significance spectrum. Right: DFT amplitudes.
|
|
The file alc.dat corresponds to the project directory alc, representing a normal SIGSPEC run without a file alc.ini. Running SigSpec alc, the resulting frequencies (screen output) are
1 freq 7.55917 sig 55.8792 rms 10.0617 csig 55.8792
2 freq 5.55706 sig 31.5539 rms 8.65888 csig 31.5539
3 freq 10.5668 sig 11.011 rms 7.81469 csig 11.011
4 freq 2.55231 sig 4.9934 rms 7.60001 csig 4.9934
Instead of the two signal components, 1-cycle-per-day aliases are identified. The significance and Fourier amplitude spectra of the dataset show the highest peak at 7.56 cycles per day, which represents a superposition of the first upper side peak of the signal at 6.56 cycles per day and the first lower side peak of the signal at 8.56 cycles per day (Fig.22. This leads to an imperfect prewhitening of the two components, and the remaining signal is detected as a third component at 9.56 cycles per day.
The alternative AntiAlC analysis is provided by the file antialc.ini, which contains the specifications
antialc:par 0.5
antialc:depth 2
antialc:adopt 1
antialc:siglimit 4
All peaks that reach at least 50% of the highest significance in the spectrum are taken into account. SIGSPEC computes two consecutive iterations, but adopts only the first of these two iterations. A sig limit of 4 is assumed for the AntiAlC calculations (contrary to the default sig limit of 5 still valid as a breakup condition for the whole procedure). Running SigSpec antialc, the screen output is
1 freq 8.56173 sig 51.5953 rms 10.0617 csig 51.5953
2 freq 6.55846 sig 46.0406 rms 8.77437 csig 46.0406
3 freq 33.7204 sig 3.9725 rms 7.48075 csig 3.9725
Both signals are recovered at a reasonable frequency accuracy. Moreover, according to the file antialc/result.dat, the amplitudes of the two signals are recovered to a satisfactory precision (7.22 mmag, 6.47 mmag).




Next: Analysis of Harmonics
Up: SigSpec User's Manual by
Previous: Time-resolved Analysis
Contents
Piet Reegen
2009-09-23
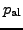 , which has to attain a value in the interval
, which has to attain a value in the interval
![$\left] 0,1\right]$](img116.png) . If the highest sig in the considered frequency range is
. If the highest sig in the considered frequency range is
![$\max\left[\mathrm{sig}\left( A\right)\right]$](img117.png) , then the sig limit is
, then the sig limit is
![$p_\mathrm{al}\max\left[\mathrm{sig}\left( A\right)\right]$](img118.png) . I.e., the AntiAlC parameter determines the sig limit for the candidate peak selection relative to the highest peak in the spectrum under consideration. Alternatively or in addition, a sig threshold for the AntiAlC candidate selection may be defined using the keyword antialc:siglimit. If neither antialc:par nor antialc:siglimit are present, the sig limit specified by siglimit in the .ini file (p.
. I.e., the AntiAlC parameter determines the sig limit for the candidate peak selection relative to the highest peak in the spectrum under consideration. Alternatively or in addition, a sig threshold for the AntiAlC candidate selection may be defined using the keyword antialc:siglimit. If neither antialc:par nor antialc:siglimit are present, the sig limit specified by siglimit in the .ini file (p.![[*]](file:/usr/share/latex2html/icons/crossref.png) ) is used for the AntiAlC candidate selection also.
) is used for the AntiAlC candidate selection also.
![\includegraphics[clip,angle=0,width=109mm, clip]{eps/antialc.dat.eps}](img127.png)
![\includegraphics[clip,angle=0,width=110mm, clip]{eps/antialc.s.eps}](img128.png)