Equivalent sig

Each linear combination is assigned an equivalent sig,

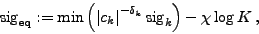$$\mathrm{sig}_{\mathrm{eq}}:=\min\left(\left\vert c_{k}\right\vert^{-\delta_{k}}\mathrm{sig}_{k}\right)-\chi \log K\: ,$$ (39)

where 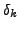$\delta_{k}$ denotes the decay parameter provided by the keyword decay, and 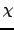$\chi$ is the combination damping, specified using the keyword cdamp. Both keywords are followed by floating-point numbers. The default values for both parameters are $1$.

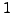Figure 1: Ratio of equivalent sig over sig of an individual signal component vs. polynomial coefficient 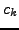$c_k$ associated to the signal component. Five graphs for different values of the decay parameter 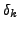$\delta _k$ are presented.

Fig.1 displays the relative sig correction with increasing coefficient 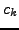$c_k$ for five different values of the decay parameter 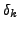$\delta _k$. Fig.2 illustrates the correction of equivalent sig with increasing number of components contributing to a linear combination 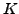$K$ for five different values of the combination damping $\chi$.

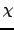Figure 2: Additive significance correction for a linear combination employing 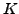$K$ different signal components. Five graphs for different values of the combination damping 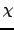$\chi$ are presented.