Limit of harmonic order

The range of harmonic orders is restricted by the parameter N, which is calculated according to

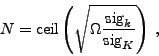$$N=\mathrm{ceil}\left(\sqrt{\Omega\frac{\mathrm{sig}_{k}}{\mathrm{sig}_{K}}}\right)\: ,$$ (37)

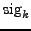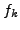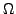where $\mathrm{sig}_{k}$ denotes the sig associated to the frequency $f_{k}$ and $\mathrm{sig}_K$ is the sig associated to the last frequency in the input file, $f_K$. If the keyword csig is set, the csig is consistently taken instead of the sig. The parameter $\Omega$ is provided by the keyword order in the file <infile>.ini, followed by a floating-point number. The default value is 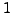$1$. 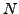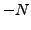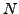Given the limit $N$, the coefficients of a linear combinations are restricted to indices from $-N$ to $N$ according to

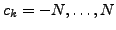$$c_{k}=-N,\ldots,N$$ (38)

.